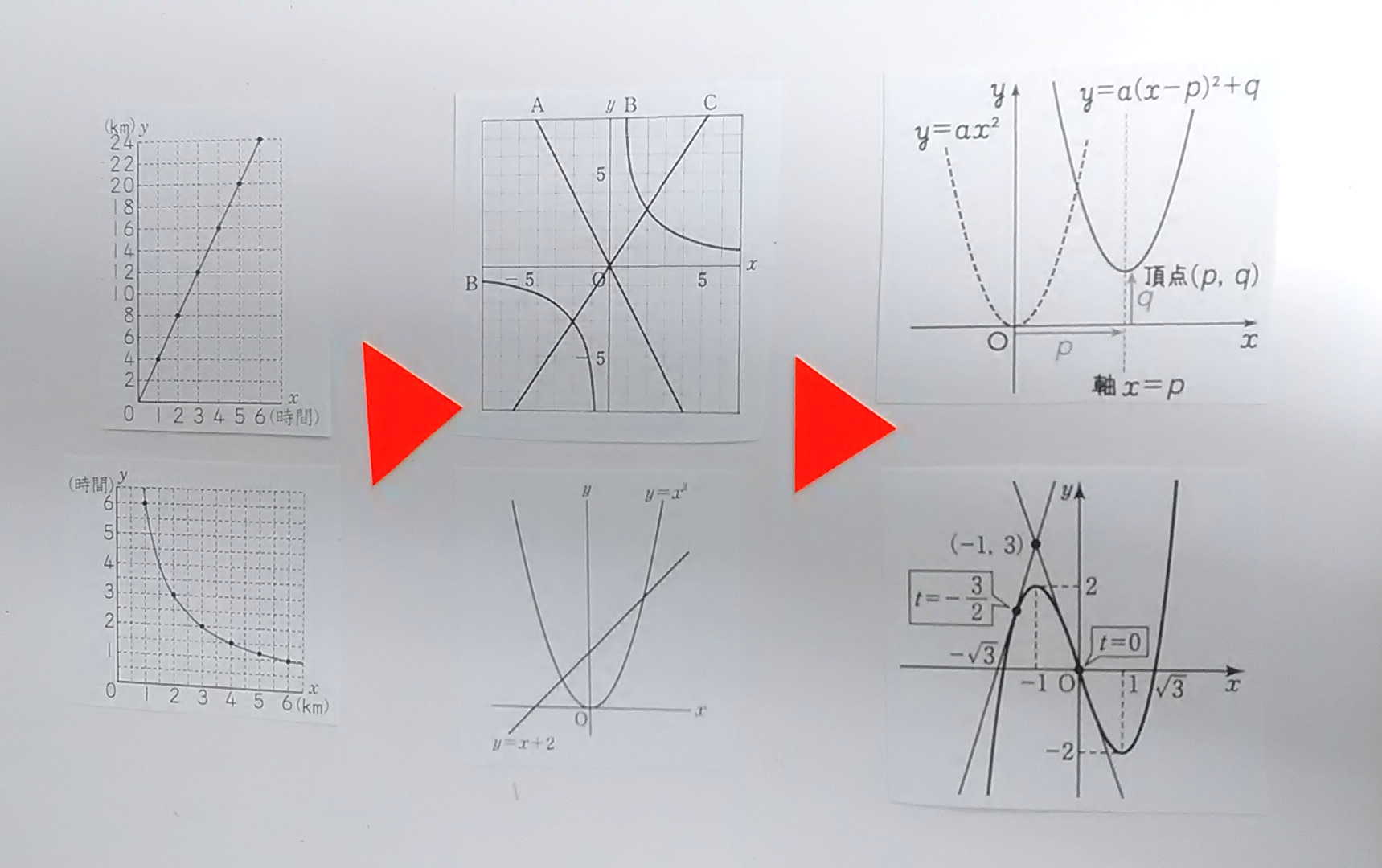
画像をご覧ください。
左はしが小学校で習うことになった比例・反比例です。
(ちなみに、真ん中が中学校の比例・反比例〈中1〉1次関数・2次関数〈中2・3〉、
右はしが高校の2次関数〈数Ⅰ〉と3次関数〈数Ⅱ〉です。)
これは算数じゃなくて、もう、しっかり数学の初歩ですよね。
今までは「変わり方調べ」という微妙なネーミング、中途半端かつ雑多な内容だったので、それよりはむしろわかりやすくなったと私は思います。
ただし、ここでつまずいてしまうと、生徒はこの分野を「分からない!難しい!キライ!!」となってしまいます。(それは、先々大きなマイナスに膨らむ可能性があります。)
中学のグラフと比べると分かりますが、負の数をまだ扱っていない小学校の算数のグラフは第1象限(縦軸・横軸とも正の数)だけに限定されています。
まずは、グラフのどこをよく見ればよいのか…それをしっかり意識させます。
縦軸・横軸がそれぞれ何を表しているのか、単位は何か、一区切りがどれだけの数量になっているのか…まさか!?と思う方もあるでしょうが、ちゃんと把握できていない場合が意外に多いのです。これが出発点です。
次に、問題文のことばと数式とグラフの相互の関係を理解できるように練習をします。このときに、速さと時間と距離の問題は具体的にイメージするのに最適ではないかと思います。
(「速さと時間」は比例、「距離と速度」「距離と時間」は反比例)
速さの文章題も「苦手」という生徒の多い分野ですが、このやり方で問題文とグラフの形と数式の関係を一気に押さえることが出来ます。
「ね?ほら、簡単にできるようになったでしょ?」と言うと嬉しそうです。
「関数では定数を小数ではなく分数でおく!」ということを徹底するにも、速さの問題は最適です。(「変わり方調べ」では、定数を小数でおかせていたので「後で間違えて困るのに、なんでこんなことするの!?」とイラっとしていました。)
単位換算で時間の問題を間違う生徒は、分数が苦手で、小数で答えようとする場合がかなりあります。時間は10進法ではなく、60進法なのだから、最初から分数で理解したら楽なのに…うまくイメージできない様子です。まめに時計を見るようにしましょう。
アテネでは、教室内のどこからでも見えるように(デジタル時計ではなく)アナログ時計を複数個掛けています。
神戸市灘区(六甲と六甲道の間)で、小学4年~高校3年の女子対象に個別指導を41年続けている
ATHENE(アテネ)の塾長 櫻井久仁子
- 投稿タグ
- 期末試験
















